- Research
- Open access
- Published:
Efficient multiparty quantum secret sharing based on a novel structure and single qubits
EPJ Quantum Technology volume 10, Article number: 29 (2023)
Abstract
Quantum secret sharing (QSS) is a significant branch of quantum cryptography and can be widely used in various applications. Quantum secret sharing schemes can be developed by utilizing different features of quantum mechanics, and quantum secure direct communication (QSDC) is an effective way to achieve secret sharing using single qubits. The utilization of QSDC offers certain benefits, such as low cost, high security, and great potential for implementation with current technologies. However, the purpose of QSDC is different from that of QSS, which causes some vulnerabilities, such as dishonest participant attacks. We discover two critical factors that affect the security of traditional protocols. Firstly, they skip a few steps from the QSDC protocol to the QSS protocol. Secondly, the participants have different privileges. This can lead to participants with more privileges engaging in potential attack behavior. In light of these issues, this study proposes a new multiparty QSS scheme to address these vulnerabilities. The proposed protocol ensures the independence of each participant and grants them equal privileges. Analysis results demonstrate that it can defend against malicious attackers, retain the advantages of the QSDC protocol, and further reduce transmission costs. It achieves an excellent balance between security and performance.
1 Introduction
Secret sharing is a crucial issue in classical cryptography and was invented independently by Shamir [1] and Blakley [2]. Secret sharing is a cryptographic primitive that capable of storing extremely sensitive and important information and can be employed for secure multiparty computation [3, 4]. The concept of secret sharing ensures that secret messages are available when all participants cooperate and cannot be obtained by a single person or participants of an insufficient number. There are usually two kinds of characters in the secret sharing scheme, one sharer and multiple receivers/participants; the sharer divides the secret into multiple pieces and passes them on to receivers. Receivers must collaborate to reconstruct the correct secret, which requires them to reveal the correct information they receive; otherwise, they cannot obtain the secret. Therefore, this scheme differs from two-party communication in that the design of this protocol must take into account not only malicious users from the outside but also dishonest group members.
In classical cryptography, the majority of significant secure protocols are founded on computational security-related complex mathematical problems; for instance, Diffie and Hellman [5] use discrete logarithm problems to construct the symmetric key exchange protocol. Afterward, Rivest, Shamir, and Adleman [6] proposed the asymmetric public-private key cryptosystem based on the factorization of large semi-prime numbers. However, in 1994, Shor [7] proposed quantum algorithms that can improve discrete logarithm and prime factorization problems significantly more efficiently than conventional algorithms. Therefore, cryptographers began searching for countermeasures to quantum computer attacks.
Quantum computers’ progress has sparked interest in quantum cryptography due to its potential for providing unconditional security. Bennett and Brassard [8] proposed the quantum key distribution (QKD) protocol (BB84). By the properties of the quantum and the no-cloning theorem [9], QKD can be resistant to the eavesdropper and guarantee the security of key transmission. The security of QKD is based on the principles of quantum physics, unlike classical key distribution, which is based on complex mathematical problems. QKD has been proven as unconditionally secure [10, 11] which means it is guaranteed to be unbreakable. The invention of QKD is unquestionably a great boost for quantum cryptography. Cryptographers are beginning to use quantum resources to develop more secure communication protocols and applications [12, 13], such as important branches of quantum secure direct transmission (QSDC) and quantum secret sharing (QSS).
Hillery, Bužek, and Berthiaume first proposed a QSS scheme [14] using the Greenberger-Horne-Zeilinger (GHZ) state for sharing classical and quantum information. Subsequently, Xiao et al. [15] extended it to multiparty quantum secret sharing (MQSS). Karlsson et al. [16] proposed another QSS protocol using two-particle quantum entanglement. Since then, several QSS schemes [17–27] have been developed. Most QSS protocols [18, 22, 23, 25, 26] use the entangled state as the medium to store the secret and some experiments [28] demonstrate its practicality. Recently, several studies [29, 30] organized the phenomenon and equations of entanglement states to improve and build the design of QSS. However, with modern technology, it is still difficult and resource-consuming to prepare for the entangled state. As the number of participants increases, the difficulty of attaining the state of multiphoton entanglement grows rapidly.
Zhang et al. [19] proposed the MQSS protocol using single photons based on QSDC [31], which brings great potential to practical implementation because it only requires single photons and local operations for sharing the secret message. Their protocols are more resource-efficient than entanglement-based protocols, and QSDC is a secure and effective method. Consequently, several cryptographers began developing QSS protocols based on the concept of single-photon. Influenced by the Zhang et al. protocol [19], the participants in most single-photon MQSS protocols form a circular loop (wherein one participant prepares the qubits and the others apply operations one by one with the participant’s order). However, this circular loop has also led to security concerns regarding these protocols. The direct addition of multiple participants to QSDC to create QSS results in a number of vulnerabilities [32, 33], including the inability to prevent the Trojan horse attack [34] and fake signal attack, which are both internal attacks. In the Trojan horse attack, for instance, one participant prepares a multiphoton quantum signal to replace the original single-photon signal and sends it to the other participant. Since the other party does not measure but only performs operations, they are unable to detect the cheater. This indicates that it is not suggested to skip the measurement stage; otherwise, it increases the security risk associated with dishonest participants.
Based on the above observations, we comprehensively analyze MQSS protocols and fundamentally design a novel and efficient QSDC-based MQSS scheme. We have discovered two perspectives that can further improve traditional designs. First, the purpose of QSDC is distinct from that of QSS, and some protocols may skip a few QSDC steps, creating a security risk. Second, because each participant has a different task to complete – some are planning operations, while others are preparing particles – this structure might be exploited by dishonest individuals. In the proposed protocol, unlike the traditional circular loop scheme, we build an independent secure communication tunnel based on QSDC between the dealer and each receiver. It makes each participant independently interact with Alice, who serves as a dealer responsible for securely sharing secrets with the participants. This design helps prevent external attacks, ensuring security and enhancing the performance of QSDC. The innovative idea is that the preparation and operation for each receiver or participant are consistent and independent, meaning that no one has privileges or unfair situations that can prevent dishonest participants from obtaining information without cooperation. In other words, the participants in the proposed protocol adopt the same privileges. Therefore, based on the novel design, we build a highly efficient and secure MQSS based on single qubits using the advantages of QSDC.
1.1 Contributions
Through the development of a new MQSS, this protocol makes three primary contributions, which are listed as follows.
-
1.
Firstly, we addressed the security issues encountered by previous studies when using QSDC to design QSS. The proposed protocol combines the efficiency of QSDC with the purpose of QSS while maintaining the security of QSDC, thereby fundamentally avoiding Trojan horse and dishonest participant attacks and providing more secure communication.
-
2.
Secondly, the transmission steps are simplified to minimize potential delays. This not only helps quantum resources maintain high fidelity, but also ensures that all participants have equal access and privileges during the process.
-
3.
Thirdly, the efficiency of this protocol surpasses other protocols in various scenarios, especially those with a larger number of participants or a greater number of messages to transmit, owing to its innovative and optimized design. Furthermore, this protocol can be implemented easily using existing quantum communication devices since it only requires single-qubit resources and does not rely on entangled resources.
2 Proposed method
This study proposes a novel multiparty quantum secret sharing protocol based on a new structure that for each participant builds an independent quantum secure direct communication path using single qubits in order to achieve an excellent balance between security and performance. This protocol is designed for highly efficient realization. This section first introduces the basic concept of the proposed protocol. Then, it describes our multiparty QSS protocol in detail and provides a step-by-step illustration of a four-party example.
2.1 Preliminary
In the proposed protocol, we use two bases called the Z-basis and the X-basis for measurement, and two operations (gates) for the secret sharing which are I and Y. The Z-basis is defined as  and
and  , and the X-basis is defined as
, and the X-basis is defined as  and
and  . All quantum gates are unitary matrices (\(UU^{*}=U^{*}U=I\)). The gates and can affect the results regardless of whether the Z-basis or X-basis is used, given the gate set \({I, Y}\).
. All quantum gates are unitary matrices (\(UU^{*}=U^{*}U=I\)). The gates and can affect the results regardless of whether the Z-basis or X-basis is used, given the gate set \({I, Y}\).
2.2 The proposed protocol
We now introduce the proposed multiparty QSS protocol in detail and give an example of four-party secret sharing, in which Alice is a dealer who shares secret with participants, Bob, Charlie, and Dave. The protocol includes the following five steps:
- Step 1.:
-
Each participant prepares \(\lceil S/N \rceil \) qubits with each qubit in one of the four randomly selected states
 in order to build quantum sequences, where S is the length of the secret and N is the number of participants. The sequences contain several decoy qubits [35, 36] for channel checking. They then separately transmit their quantum sequences to Alice.
in order to build quantum sequences, where S is the length of the secret and N is the number of participants. The sequences contain several decoy qubits [35, 36] for channel checking. They then separately transmit their quantum sequences to Alice. - Step 2.:
-
Alice checks the channel with all participants by the decoy qubits. Alice randomly chooses sufficient qubits and asks all the participants to publish the basis and states of these qubits. Alice uses the same basis to measure and compare the results. If the error rate is higher than the threshold, she requests that the sequence be resent until it passes the channel checking.
- Step 3.:
-
After that, Alice joins these sequences together and reorders qubits. Alice then encodes her secret into the sequence by using I and Y gates according to her message “0” and “1”, respectively, and divides it into N sequences according to the number of participants. She then inserts the decoy qubits [35, 36] into these sequences and sends them back to all participants.
- Step 4.:
-
After all participants received the sequences from Alice, Alice published the positions and states of the decoy qubits. All participants can check the channel. Alice publishes the order of the qubits if the error rate is below the threshold; else, the communication is terminated and restarted using a different channel.
- Step 5.:
-
All participants have to cooperate to recover the secret by exchanging the information on original quantum states (i.e.
 ).
).
Let us take an example with a dealer and three participants. A dealer Alice wants to share three bits secret to participants Bob, Charlie, and Dave, and all participants prepare one decoy qubit for the simplest case.
- Step 1::
-
Each one of Bob, Charlie, and Dave prepares one qubit in
 ,
,  and
and  , respectively, which calls qubits \(B_{1}\), \(C_{1}\) and \(D_{1}\) in sequences SB, SC and SD, respectively. After that, they also insert one decoy qubit into SB, SC and SD in states
, respectively, which calls qubits \(B_{1}\), \(C_{1}\) and \(D_{1}\) in sequences SB, SC and SD, respectively. After that, they also insert one decoy qubit into SB, SC and SD in states  ,
,  and
and  , which are called decoys \(B_{d}\), \(C_{d}\) and \(D_{d}\), respectively. They then send their sequences to Alice.
, which are called decoys \(B_{d}\), \(C_{d}\) and \(D_{d}\), respectively. They then send their sequences to Alice. - Step 2::
-
Alice randomly chooses one qubit from each sequence (in this case, we suppose that she chose the decoy qubit). After channel checking, she drops those qubits (Steps 1 and 2 are shown in Fig. 1).
- Step 3::
-
Alice combines three sequences to be a sequence and reorders the qubits and performs I, Y, and Y on qubits \(B_{1}\), \(C_{1}\) and \(D_{1}\), respectively. In this way, the states of \(B_{1}\), \(C_{1}\) and \(D_{1}\) become
 ,
,  and
and  . Alice then inserts another three decoy qubits, which are called decoys \(B'_{d}\), \(C'_{d}\) and \(D'_{d}\), and divides it into three sequences and sends them back to Bob, Charlie, and Dave.
. Alice then inserts another three decoy qubits, which are called decoys \(B'_{d}\), \(C'_{d}\) and \(D'_{d}\), and divides it into three sequences and sends them back to Bob, Charlie, and Dave. - Step 4::
-
Bob, Charlie and Dave check the channel with Alice through the decoy qubits. She then publishes the order of the qubit (Steps 3 to 4 are shown in Fig. 2).
- Step 5::
-
Each participant must cooperate to recover the secret by exchanging their bases and secret from Alice. They can read out the gates I, Y and Y from \(B_{1}\), \(C_{1}\) and \(D_{1}\) by comparing the original state
 ,
, 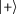 and
and  with
with  ,
,  and
and  , so they can learn that Alice’s message is “011”. Step 5 is shown in Fig. 3.
, so they can learn that Alice’s message is “011”. Step 5 is shown in Fig. 3.
In summary, our approach essentially builds the QSS framework on top of QSDC. It can be seen as Alice dividing her message into N parts for the participants, who need to collectively participate in the decryption process to reconstruct the message. Therefore, excellent implementation approaches can serve as effective foundations for our protocol. For instance, the concepts of device-independent QSDC (DI-QSDC) [37] and measurement-device-independent QSDC (MDI-QSDC) [38] originated from the measurement-device-independent quantum key distribution (MDI-QKD) proposed by Lo et al. [39] in 2012. MDI-QKD addresses vulnerabilities associated with imperfect devices, enabling QKD operations to be completed with the inclusion of an untrusted third party. The QSDC implementation [40] has enabled transmission distances greater than 100 kilometers as of 2022. Researchers have also attempted to apply MDI techniques to MQSS [41], conducting successful entanglement swapping operations using this method. Furthermore, other researchers have employed the techniques of continuous-variable quantum key distribution (CV-QKD) [42], a technology that has been in development since 2002 [43]. CV-QKD enables point-to-point key distribution in insecure quantum channels. In 2020, more suitable CV-QKD techniques for long-distance transmission were developed [44]. Currently, some researchers have applied CV-QKD techniques directly to QSS methods [45, 46] to achieve the goal of QSS without the need for an additional QSDC step. Regardless of the implementation approach, it can be combined with theoretical protocol frameworks. Hence, it is crucial to simultaneously develop efficient and secure protocol frameworks in theory and efficient implementation methods.
3 Security analysis
This section discusses the security of the proposed protocol. There are two kinds of attacks: external and internal attacks. The external attack supposes that some external attackers want to steal some information without being discovered. Internal attacks occur when some of the participants want to recover secret information from the dealer without cooperating with other participants.
3.1 External attack
Suppose Eve is an external eavesdropper. She desires to receive Alice’s messages without authorization. Therefore, she needs to know the initial state of Bob and Charlie’s preparation qubit and the operation Alice performs. She then intercepted the qubits encoded by Alice to extract the information. The following are the types of attacks that Eve may take.
3.1.1 Intercept-and-resend attack
In this attack, Eve first intercepts the qubits sent by Bob and Charlie. Next, she measures the qubits and sends them back to Alice. However, Eve does not know the basis of each qubit, she may randomly choose the Z-basis or the X-basis to measure. Therefore, the chance of her choosing the correct basis for each qubit is \(1/2\). If Eve chooses the wrong basis, Alice still has a \(1/2\) chance of catching her. Suppose the state of the qubit Eve intercepts is  . If Eve chooses the X-basis to measure because
. If Eve chooses the X-basis to measure because  , Eve has a 50% chance of measuring
, Eve has a 50% chance of measuring  or
or  . When Alice measures with the Z-basis, she has a 50% chance of measuring
. When Alice measures with the Z-basis, she has a 50% chance of measuring  or
or  because
because  and
and  . If Alice’s measurement is
. If Alice’s measurement is  , she can discover Eve. Therefore, Alice has a \(1-(\frac{3}{4})^{C}\) chance of discovering the eavesdropper, and C is the number of the decoy qubits [35, 36]. If \(C = 5\), the probability of Eve being caught is 0.762. If \(C = 33\), the probability of Eve being caught will rise to 0.99992. The caught probability of Eve rises rapidly. Therefore, when C is large enough, Alice will be able to catch Eve.
, she can discover Eve. Therefore, Alice has a \(1-(\frac{3}{4})^{C}\) chance of discovering the eavesdropper, and C is the number of the decoy qubits [35, 36]. If \(C = 5\), the probability of Eve being caught is 0.762. If \(C = 33\), the probability of Eve being caught will rise to 0.99992. The caught probability of Eve rises rapidly. Therefore, when C is large enough, Alice will be able to catch Eve.
3.1.2 Entangling attack
In this attack, Eve may want to entangle an ancillary qubit to a quantum system. Eve uses gate \(U_{e}\) to entangle qubit  into the quantum system during the transmission. The gate \(U_{e}\) is defined as follows:
into the quantum system during the transmission. The gate \(U_{e}\) is defined as follows:

where  ,
,  ,
,  , and
, and  are four states determined by gate \(U_{e}\) as well as \(\Vert a \Vert ^{2}+ \Vert b \Vert ^{2}=1\) and \(\Vert c \Vert ^{2}+ \Vert d \Vert ^{2}=1\). If Eve wants to avoid detection, \(U_{e}\) must satisfy \(a=d=1\), \(b=c=0\), and
are four states determined by gate \(U_{e}\) as well as \(\Vert a \Vert ^{2}+ \Vert b \Vert ^{2}=1\) and \(\Vert c \Vert ^{2}+ \Vert d \Vert ^{2}=1\). If Eve wants to avoid detection, \(U_{e}\) must satisfy \(a=d=1\), \(b=c=0\), and  . As a result, the states of the qubit
. As a result, the states of the qubit  are always the same, no matter what the states of the first qubit are. Therefore, Eve cannot read any information from the entanglement.
are always the same, no matter what the states of the first qubit are. Therefore, Eve cannot read any information from the entanglement.
3.2 Internal attack
In the QSS protocols, it needs to take into account the internal attacks that assume there are dishonest participants in the group. Internal attacks involve two attacks, which are the Trojan horse and dishonest participants. Any dishonest participants could potentially launch an attack against the other participants by using device differences and vulnerabilities of the protocol, both of which are described in the following paragraphs. This subsection describes how the proposed protocol prevents this kind of attack.
3.2.1 Trojan horse attack
In the attack described by Gisin et al. [34], the dishonest participant replaces single photons with multiple photons. This attack exploits the stages of the protocol where channel checking based on single photons is not performed. Additionally, all participants are required to transfer their qubit sequences to others without measurement, creating vulnerabilities. However, in the proposed protocol, all participants directly interact with Alice, and each transmission undergoes thorough checking. Alice employs decoy qubits and performs measurements on the qubit states to verify the honesty of the participants. This design effectively protects against Trojan horse attacks, ensuring the security of the protocol.
3.2.2 Dishonest participants’ attack
Some participants may cooperate to exchange their information and qubits to recover the secret from Alice. However, they do not know the order of the qubit sequences, and all participants independently face Alice. The dishonest participants have to cooperate with others. In this way, we can also defend against this kind of attack.
In short, the protocol is resistant to external attacks as well as internal attacks. By having both sides prepare qubits, the protocol can effectively resist internal attacks. Because one party does not know how to obtain the original state and the order of the other party’s qubits, they must cooperate to reconstruct the message.
4 Efficiency analysis
In this section, this study compares the efficiency with six different MQSS protocols. There are three protocols using single qubits and three protocols using entangled qubits. Here, the single qubits protocols are Zhang et al. [18] and its improved versions [32, 33]. In this case, we note the importance of channel checking. We choose three protocols using entangled qubits [14, 23, 25]. Entanglement is a method that has been frequently utilized in recent years, but it also requires more resources. These protocols used different properties of quantum physics which can represent the different kinds of branches in MQSS.
For the efficiency analysis, we have to define three variables: S, N, and C. In our scenario, S is the length of the secret. N is the number of participants excluding the dealer Alice. C is the number of decoy qubits in each channel checking. The decoy qubits of all protocols for channel checking almost conformed to the detection rate of BB84. For the channel checking process, the experiments assume that C is set to 50. This means that we can detect the presence of an eavesdropper with a probability of \(1-(\frac{3}{4})^{50}\), which exceeds 99.9999%. Thus, there is an extremely high likelihood of identifying any unauthorized listeners.
There are six important evaluations used to compare the efficiencies of each protocol, including the number of used qubits, the number of qubit transmissions, the number of projective measurements, the number of checking qubits, the number of operations, and the transmission delay. The number of used qubits means each qubit utilized in the protocol, as well as the number of entangled states. The number of qubit transmissions means the count of all qubit transmissions. The total number of projective measures means each measurement is tallied. The number of checking qubits is the number of decoy qubits used for channel checking. The number of operations means all the quantum gates performed are counted. Transmission delay is an important evaluation. If the transmission is dependent, which means each participant has to wait for another’s transmission, the transmission delay will increase with the number of participants. Table 1 displays the results of comparisons with different protocols. Based on these six evaluations, the number of qubit transmissions has emerged as a significant factor in resource consumption and efficiency analysis. Figure 4 visually presents the performance comparison between the proposed protocol and others, specifically highlighting the number of qubit transmissions as a crucial measure of resource utilization. Our protocol noticeably performs better as the length of the shared secret or the number of participants increases.
Illustration of the comparison results. N ranges from 2 to 10, S ranges from 100 to 3000, and \(C=50\). We average all the results for each value of N to obtain the number of qubit transmissions, which shows the resource usage of each participant. The focus of this figure is on the number of qubit transmissions as a crucial measure of resource utilization. Our protocol demonstrates superior performance as the shared secret length increases or when more participants are involved
- Qin et al.’s protocol [33]::
-
We discuss the performance of the last improved version [33] of Zhang et al.’s [19] protocol because it is more secure. They take the \(S+NC\) qubits for secret sharing and channel checking, where \(N\times C\) denotes that they have to check the channel securely to defend the eavesdropper and dishonest Bob in every transmission. It performs the \(N(S+C)\) number of qubit transmission, where \(S+C\) is the number of qubits in a sequence and N is the number of transmissions between all participants and the dealer. The performance is good in the original version [19], but it is insecure. In spite of this, our protocol is more effective in a condition with more participants and a longer length of secret message.
- Hillery et al. [14] protocol::
-
They use a GHZ entangled state to distribute a shared key to all participants or share a qubit through teleportation. In this way, they take double the amount of the entangled state than the secret length S. An advantage of this protocol is that they can take only one channel checking for all participants, which means C qubits are required. However, most resources and the number of qubit transmissions are required for distributing entangled qubits.
- Chou et al. [23] protocol::
-
They improved the transmission rate from two bits to four bits based on Zhang et al.’s protocol [18]. Its performance is also better than other protocols. However, this protocol asks that Alice needs a more powerful quantum machine than all participants, and Alice has to help each participant share the EPR pair [47] by entanglement swapping, which will also lead to a high transmission delay.
- Song et al. [25] protocol::
-
They improved the cost of qubits from \(N+1\) EPR pairs [47] to N EPR pairs [47]. However, its performance is similar to the protocol of Chou et al. [23]. It also requires Alice to have a quantum machine that is more powerful than all the participants, and each participant gets a message through entanglement swapping, which causes high transmission delays.
- Proposed protocol::
-
The advantages of our protocol are that it becomes more efficient as the number of participants and length of secret increase. Figure 4 demonstrates that when the length of the secret grows, the qubit transmission numbers of the majority of protocols increase rapidly. It can discover that the proposed protocol can significantly use fewer resources to share the same length of a secret. In addition, our protocol can be parallel, in which all participants can transfer their own sequence without waiting for others. Other protocols have to wait for Alice and other participants, resulting in a high transmission delay.
5 Discussions and conclusions
In this study, we make a first attempt to design a novel structure based on QSDC to construct a multiparty quantum secret sharing protocol. A variety of MQSS schemes have been proposed based on different quantum properties such as Bell states, GHZ states, different quantum operations, etc., to facilitate the quantum secure communication and computation. Each developed protocol has its own benefits and limitations. The QSDC based on single photons is a high-performance approach that can transfer a secret message between two parties. However, the purpose of QSDC is different from the purpose of QSS, so when building QSS based on QSDC needs to address the security issue more carefully. The proposed scheme treats each receiver independently and designs a QSDC protocol between the dealer and each participant to build the MQSS protocol. It can guarantee that every communication channel between participants is unconditionally secure. Furthermore, every participant has the same task and privilege, which means they perform the same operations and no one has special abilities in order to prevent dishonest participants. From the security analysis, our protocols based on these two designs can defend against all possible internal and external attacks. In this way, the MQSS protocol proposed in this article can keep all the advantages of the QSDC. According to efficiency analysis, our performance is better than other traditional protocols and does not require entanglement states, which are still expensive currently. This structure has great potential for more practical in use. In future work, we expect to construct a more efficient MQSS protocol and extend the protocol to the design of the threshold QSS.
Availability of data and materials
Not applicable.
Abbreviations
- QKD:
-
Quantum Key Distribution
- QSS:
-
Quantum Secret Sharing
- MQSS:
-
Multiparty QSS
- QSDC:
-
Quantum Secure Direct Communication
References
Shamir A. How to share a secret. Commun ACM. 1979;22(11):612–3.
Blakley GR. Safeguarding cryptographic keys. In: Managing requirements knowledge, international workshop on. Los Alamitos: IEEE Comput. Soc.; 1979. p. 313–.
Cramer R, Damgård I, Maurer U. General secure multi-party computation from any linear secret-sharing scheme. In: Advances in cryptology XEUROCRYPT 2000: international conference on the theory and application of cryptographic techniques bruges. Proceedings. vol. 19. Belgium. May 14–18, 2000. Berlin: Springer; 2000. p. 316–34.
Parakh A, Kak S. Space efficient secret sharing for implicit data security. Inf Sci. 2011;181(2):335–41.
Diffie W, Hellman ME. New directions in cryptography. IEEE Trans Inf Theory. 1976;22(6):644–54.
Rivest RL, Shamir A, Adleman L. A method for obtaining digital signatures and public-key cryptosystems. Commun ACM. 1978;21(2):120–6.
Shor PW. Algorithms for quantum computation: discrete logarithms and factoring. In: 35th annual symposium on foundations of computer science. 1994. p. 124–34.
Bennett CH, Brassard G. Quantum cryptography: public key distribution and coin tossing. In: Proceedings of the IEEE international conference on computers, systems, and signal processing. Bangalore. 1984. p. 175–9.
Wootters WK, Zurek WH. A single quantum cannot be cloned. Nature. 1982;299:802–3.
Lo H-K, Chau H-F. Unconditional security of quantum key distribution over arbitrarily long distances. Science. 1999;283:2050–6.
Shor PW, Preskill J. Simple proof of security of the BB84 quantum key distribution protocol. Phys Rev Lett. 2000;85:441–4.
Zhang H, Ji Z, Wang H, Wu W. Survey on quantum information security. China Commun. 2019;16(10):1–36.
Kuang R, Perepechaenko M. Quantum encryption with quantum permutation pad in IBMQ systems. EPJ Quantum Technol. 2022;9(1):26.
Hillery M, Bužek V, Berthiaume A. Quantum secret sharing. Phys Rev A. 1999;59:1829–34.
Xiao L, Long G-L, Deng F-G, Pan J-W. Efficient multiparty quantum-secret-sharing schemes. Phys Rev A. 2004;69:052307.
Karlsson A, Koashi M, Imoto N. Quantum entanglement for secret sharing and secret splitting. Phys Rev A. 1999;59:162–8.
Guo G-P, Guo G-C. Quantum secret sharing without entanglement. Phys Lett A. 2003;310:247–51.
Zhang Z-J, Man Z-X. Multiparty quantum secret sharing of classical messages based on entanglement swapping. Phys Rev A. 2005;72:022303.
Zhang Z-J, Li Y, Man Z-X. Multiparty quantum secret sharing. Phys Rev A. 2005;71(4):044301.
Deng F-G, Zhou P, Li X-H, Zhou C-Y. Efficient multiparty quantum secret sharing with Greenberger-Horne-Zeilinger states. Chin Phys Lett. 2006;23:1084–7.
Deng F-G, Zhou H-Y, Long GL. Circular quantum secret sharing. J Phys A, Math Gen. 2006;39(45):14089.
Hwang T, Hwang C-C, Li C-M. Multiparty quantum secret sharing based on GHZ states. Phys Scr. 2011;83:045004.
Chou Y-H, Chen C-Y, Fan R-K, Chao H-C, Lin F-J. Enhanced multiparty quantum secret sharing of classical messages by using entanglement swapping. IET Inf Secur. 2012;6(2):84–92.
Mohajer R, Eslami Z. Quantum secret sharing using single states. In: 2016 8th international symposium on telecommunications (IST). Los Alamitos: IEEE; 2016. p. 174–7.
Song Y, Li Y, Wang W. Multiparty quantum direct secret sharing of classical information with Bell states and Bell measurements. Int J Theor Phys. 2018;57:1559–71.
Zhang K-J, Zhang X, Jia H-Y, Zhang L. A new n-party quantum secret sharing model based on multiparty entangled states. Quantum Inf Process. 2019;18:1–15.
Chou Y-H, Zeng G-J, Chen X-Y, Kuo S-Y. Multiparty weighted threshold quantum secret sharing based on the Chinese remainder theorem to share quantum information. Sci Rep. 2021;11(1):6093.
Tittel W, Zbinden H, Gisin N. Experimental demonstration of quantum secret sharing. Phys Rev A. 2001;63(4):042301.
Shi R-H. Useful equations about Bell states and their applications to quantum secret sharing. IEEE Commun Lett. 2019;24(2):386–90.
Musanna F, Kumar S. Quantum secret sharing using GHZ state qubit positioning and selective qubits strategy with simulation analysis. Int J Theor Phys. 2022;61(10):255.
Deng F-G, Long G-L. Secure direct communication with a quantum one-time pad. Phys Rev A. 2004;69(5):052319.
Deng F-G, Li X-H, Zhou H-Y, Zhang Z-J. Improving the security of multiparty quantum secret sharing against Trojan horse attack. Phys Rev A. 2005;72(4):044302.
Qin S-J, Gao F, Wen Q-Y, Zhu F-C. Improving the security of multiparty quantum secret sharing against an attack with a fake signal. Phys Lett A. 2006;357(2):101–3.
Gisin N, Ribordy G, Tittel W, Zbinden H. Quantum cryptography. Rev Mod Phys. 2002;74:145–95.
Hwang W-Y. Quantum key distribution with high loss: toward global secure communication. Phys Rev Lett. 2003;91(5):057901.
Li C-Y, Zhou H-Y, Wang Y, Deng F-G. Secure quantum key distribution network with Bell states and local unitary operations. Chin Phys Lett. 2005;22(5):1049.
Zhou L, Sheng Y-B, Long G-L. Device-independent quantum secure direct communication against collective attacks. Sci Bull. 2020;65(1):12–20.
Zhou Z, Sheng Y, Niu P, Yin L, Long G, Hanzo L. Measurement-device-independent quantum secure direct communication. Sci China, Phys Mech Astron. 2020;63(3):230362.
Lo H-K, Curty M, Qi B. Measurement-device-independent quantum key distribution. Phys Rev Lett. 2012;108(13):130503.
Zhang H, Sun Z, Qi R, Yin L, Long G-L, Lu J. Realization of quantum secure direct communication over 100 km fiber with time-bin and phase quantum states. Light: Sci Appl. 2022;11(1):83.
Zhang T, Zhou L, Zhong W, Sheng Y-B. Multiple-participant measurement-device-independent quantum secret sharing protocol based on entanglement swapping. Laser Phys Lett. 2023;20(2):025203.
Pirandola S, Andersen UL, Banchi L, Berta M, Bunandar D, Colbeck R, Englund D, Gehring T, Lupo C, Ottaviani C et al.. Advances in quantum cryptography. Adv Opt Photonics. 2020;12(4):1012–236.
Grosshans F, Grangier P. Continuous variable quantum cryptography using coherent states. Phys Rev Lett. 2002;88(5):057902.
Liao Q, Xiao G, Xu C-G, Xu Y, Guo Y. Discretely modulated continuous-variable quantum key distribution with an untrusted entanglement source. Phys Rev A. 2020;102(3):032604.
Liao Q, Liu H, Zhu L, Guo Y. Quantum secret sharing using discretely modulated coherent states. Phys Rev A. 2021;103(3):032410.
Liao Q, Liu H, Gong Y, Wang Z, Peng Q, Guo Y. Practical continuous-variable quantum secret sharing using plug-and-play dual-phase modulation. Opt Express. 2022;30(3):3876–92.
Einstein A, Podolsky B, Rosen N. Can quantum-mechanical description of physical reality be considered complete? Phys Rev A. 1935;47:777–80.
Funding
This work was supported in part by the National Science and Technology Council, Taiwan, under Grants 109-2222-E-005-002-MY3, 110-2627-M-002-002, 111-2218-E-005-007-MBK, 111-2221-E-260-014-MY2, 111-2627-M-002-001, 111-2119-M-033-001, and 111-2222-E-197-001-MY2; and in part by the National Center for Theoretical Sciences of Taiwan.
Author information
Authors and Affiliations
Contributions
S.-Y. K. designed the project and took the lead in writing the manuscript. K.-C. T. and C.-C. Y. developed the method and performed security analysis and consumption comparison. Y.-H. C. designed and directed the project. All authors discussed the method and results and commented on the manuscript.
Corresponding author
Ethics declarations
Competing interests
The authors declare no competing interests.
Additional information
Publisher’s Note
Springer Nature remains neutral with regard to jurisdictional claims in published maps and institutional affiliations.
Rights and permissions
Open Access This article is licensed under a Creative Commons Attribution 4.0 International License, which permits use, sharing, adaptation, distribution and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons licence, and indicate if changes were made. The images or other third party material in this article are included in the article’s Creative Commons licence, unless indicated otherwise in a credit line to the material. If material is not included in the article’s Creative Commons licence and your intended use is not permitted by statutory regulation or exceeds the permitted use, you will need to obtain permission directly from the copyright holder. To view a copy of this licence, visit http://creativecommons.org/licenses/by/4.0/.
About this article
Cite this article
Kuo, SY., Tseng, KC., Yang, CC. et al. Efficient multiparty quantum secret sharing based on a novel structure and single qubits. EPJ Quantum Technol. 10, 29 (2023). https://doi.org/10.1140/epjqt/s40507-023-00186-x
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjqt/s40507-023-00186-x
 in order to build quantum sequences, where S is the length of the secret and N is the number of participants. The sequences contain several decoy qubits [
in order to build quantum sequences, where S is the length of the secret and N is the number of participants. The sequences contain several decoy qubits [ ).
). ,
,  and
and  , respectively, which calls qubits
, respectively, which calls qubits  ,
,  and
and  , which are called decoys
, which are called decoys 
 ,
,  and
and  . Alice then inserts another three decoy qubits, which are called decoys
. Alice then inserts another three decoy qubits, which are called decoys 
 ,
, 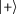 and
and  with
with  ,
,  and
and  , so they can learn that Alice’s message is “011”. Step 5 is shown in Fig.
, so they can learn that Alice’s message is “011”. Step 5 is shown in Fig. 
