- Research
- Open access
- Published:
Creation of two-dimensional Coulomb crystals of ions in oblate Paul traps for quantum simulations
EPJ Quantum Technology volume 2, Article number: 2 (2015)
Abstract
We develop the theory to describe the equilibrium ion positions and phonon modes for a trapped ion quantum simulator in an oblate Paul trap that creates two-dimensional Coulomb crystals in a triangular lattice. By coupling the internal states of the ions to laser beams propagating along the symmetry axis, we study the effective Ising spin-spin interactions that are mediated via the axial phonons and are less sensitive to ion micromotion. We find that the axial mode frequencies permit the programming of Ising interactions with inverse power law spin-spin couplings that can be tuned from uniform to  with DC voltages. Such a trap could allow for interesting new geometrical configurations for quantum simulations on moderately sized systems including frustrated magnetism on triangular lattices or Aharonov-Bohm effects on ion tunneling. The trap also incorporates periodic boundary conditions around loops which could be employed to examine time crystals.
with DC voltages. Such a trap could allow for interesting new geometrical configurations for quantum simulations on moderately sized systems including frustrated magnetism on triangular lattices or Aharonov-Bohm effects on ion tunneling. The trap also incorporates periodic boundary conditions around loops which could be employed to examine time crystals.
1 Introduction
Using a digital computer to predict the ground state of complex many-body quantum systems, such as frustrated magnets, becomes an intractable problem when the number of spins becomes too large. The constraints on the system’s size become even more severe if one is interested in the (nonequilibrium) quantum dynamics of the system. Feynman proposed the use of a quantum-mechanical simulator to efficiently solve these types of quantum problems [1]. One successful platform for simulating lattice spin systems is the trapped ion quantum simulator, which has already been used to simulate a variety of scenarios [2–13]. In one realization [14], ions are cooled in a trap to form a regular array known as a Coulomb crystal and the quantum state of each simulated spin can be encoded in the internal states of each trapped ion. Laser illumination of the entire crystal then can be used to program the simulation (spin-spin interactions, magnetic fields, etc.) via coupling to phonon modes, and readout of the internal ion states at the end of the simulation corresponds to a projective measurement of each simulated spin on the measurement basis.
To date, the largest number of spins simulated in this type of device is about 300 ions trapped in a rotating approximately-triangular lattice in a Penning trap [15]. In that experiment, a spin-dependent optical dipole force was employed to realize an Ising-type spin-spin coupling with a tunable power law behavior. Although the Penning trap can implement a transverse magnetic field to rotate the ions, the Penning trap simulator was not able to apply a time-dependent transverse magnetic field to perform certain desirable tasks such as the adiabatic state preparation of the ground state of a frustrated magnet. The reason why the transverse field has not been tried yet is that the Penning trap cannot be cooled to the ground state for the phonons, and the presence of phonons causes problems with the quantum coherence of the system. Improvements of the experiment are currently in progress which may allow for a transverse field Ising model simulation in the near future. The complexity of the Penning trap apparatus also creates a barrier to adoption and therefore does not seem to be as widespread as radio-frequency (RF) Paul traps.
Experiments in linear Paul traps have already performed a wide range of different quantum simulations within a one-dimensional linear crystal [2–9]. The linear Paul trap is a mature architecture for quantum information processing, and quantum simulations in linear chains of ions have benefited from a vast toolbox of techniques that have been developed over the years. Initially, the basic protocol [14] was illustrated in a two-ion trap [2], which was followed by a study of the effects of frustration in a three-ion trap [3]. These experiments were scaled up to larger systems first for the ferromagnetic case [4] and then for the antiferromagnetic case [5]. Effective spin Hamiltonians were also investigated using a Trotter-like stroboscopic approach [6]. As it became clear that the adiabatic state preparation protocol was difficult to achieve in these experiments, ion trap simulators turned to spectroscopic measurements of excited states [7] and global quench experiments to examine Lieb-Robinson bounds and how they change with long-range interactions (in both Ising and XY models) [8, 9].
It is therefore desirable to be able to use the demonstrated power of the Paul trap systems to extend access to the 2D physics that is native to the Penning trap systems. However, extension of this technology to higher dimensions is hampered by the fact that most ions in 2D and 3D Coulomb crystals no longer sit on the RF null. This leads to significant micromotion at the RF frequency and can couple to the control lasers through Doppler shifts if the micromotion is not perpendicular to the laser-illumination direction, leading to heating and the congestion of the spectrum by micromotion sidebands. However, the micromotion may not cause as many problems as previously thought. It has recently been shown that a robust quantum gate can be implemented even in the presence of large micromotion [16].
In an effort to utilize the desirable features of the Paul trap system to study the 2D physics, arrays of Paul traps are being pursued [17–22]. It has also been shown that effective higher-dimensional models may be programmed into a simulator with a linear crystal if sufficient control of the laser fields can be achieved [23]. In this article, we study an alternative approach to applying Paul traps to the simulation of frustrated 2D spin lattices. We consider a Paul trap with axial symmetry that forms an oblate potential, squeezing the ions into a 2D crystal. The micromotion in this case is purely radial due to symmetry, and lasers that propagate perpendicular to the crystal plane will therefore not be sensitive to Doppler shifts from micromotion. We study the parameter space of a particular model trap geometry to find the crystal structures, normal modes, and programmable spin-spin interactions for 2D triangular crystals in this trap. We find a wide parameter space for making such crystals, and an Ising spin-spin interaction with widely-tunable range, suitable for studying spin frustration and dynamics on triangular lattices with tens of ions.
In the future, we expect the simulation of larger systems to be made possible within either the Penning trap, or in linear Paul traps that can stably trap large numbers of ions. It is likely that spectroscopy of energy levels will continue to be examined, including new theoretical protocols [24]. Designing adiabatic fast-passage experiments along the lines of what needs to be done for the nearest-neighbor transverse field Ising model [25] might improve the ability to create complex quantum ground states. Motional effects of the ions are also interesting, such as tunneling studies for motion in the quantum regime [26]. It is also possible that novel ideas like time crystals [27, 28] could be tested (although designing such experiments might be extremely difficult).
The organization of the remainder of the paper is as follows: In Section 2, we introduce and model the potential energy and effective trapping pseudopotential for the oblate Paul trap. In Section 3, we determine the equilibrium positions and the normal modes of the trapped ions, with a focus on small systems and how the geometry of the system changes as ions are added in. In Section 4, we show representative numerical results for the equilibrium positions and the normal modes. We then show numerical results for the effective spin-spin interactions that can be generated by a spin-dependent optical dipole force. In Section 5, we provide our conclusions and outlook.
2 Oblate Paul trap
The quantum simulator architecture we study here is based on a Paul trap with an azimuthally symmetric trapping potential that has significantly stronger axial confinement than radial confinement, which we call an ‘oblate Paul trap’ since the resulting effective potential resembles an oblate ellipsoid. As we show below, this can create a Coulomb crystal of ions that is a (finite) two-dimensional triangular lattice. 2D Coulomb crystals in oblate Paul traps have been studied since the 1980’s and were used, for instance, by the NIST Ion Storage Group [29] to study spectroscopy [30, 31], quantum jumps [32], laser absorption [33, 34] and cooling processes [35]. 2D crystals in oblate Paul traps have also been studied by other groups both experimentally [36, 37] and theoretically [38–44].
The particular oblate Paul trap we study has DC ‘end cap’ electrodes above and below a central radio-frequency (RF) ring, as depicted in Figure 1. The trap we propose uses modern microfabrication and lithography technology (manufactured by Translume, Ann Arbor, MI) to realize the DC end cap electrodes as surface features on a monolithic fused silica substrate, providing native mechanical indexing and easier optical access to the ions than discrete end cap traps. Similar to Penning traps, oblate Paul traps can be used to study frustration effects when the lattice of ions has multiple rings. However in a Penning trap, the lattice of ions is rotating and the ions are in a strong magnetic field, which can add significant complications. In an oblate Paul trap, the lattice of ions is stationary except for the micromotion of each ion about its equilibrium positions (which is confined to the plane of the crystal by symmetry) and the qubits can be held in nearly zero magnetic field, permitting the use of the  ‘clock state’ used in linear Paul trap quantum simulators [3]. For trapped ions in a crystal that is a single polygon (
‘clock state’ used in linear Paul trap quantum simulators [3]. For trapped ions in a crystal that is a single polygon ( ), we can study periodic boundary conditions applied to a linear chain of trapped ions in the linear Paul quantum simulators. Oblate Paul traps can also potentially be used to perform experiments that are similar to those recently exploring the Aharonov-Bohm effect [26] with more ions.
), we can study periodic boundary conditions applied to a linear chain of trapped ions in the linear Paul quantum simulators. Oblate Paul traps can also potentially be used to perform experiments that are similar to those recently exploring the Aharonov-Bohm effect [26] with more ions.
Top view of the proposed oblate Paul trap. The ions are trapped in the through hole in the center, which is magnified in a three-dimensional image in panel (b). The diameter and height of the RF ring electrodes is 500 μm and 140 μm, respectively. Radial optical access tunnels are visible in (b) and will contribute to the breaking of rotational symmetry, but play no other role in this analysis. Electrodes 1-4 are labeled in both panels and the RF ring is shown in panel (b). The origin is defined to be at the center of the trap. For our calculations, we hold all four electrodes on either the top or bottom face at the same potential as the segmenting is for compensation of stray fields in the experiment and plays no role in the ion crystal structure.
It is well known that Maxwell’s equations forbid the possibility to use a static electric field to trap charged particles in free space through Earnshaw’s theorem. However, a static electric field can create a saddle-point, which confines the charged particles in some directions and deconfines them in the other directions. A static electric field that provides a saddle-point is

where A is a constant and  are the perpendicular unit vectors with
are the perpendicular unit vectors with  . Using a static electric field with a saddle-point, both Penning and radio-frequency (RF) Paul traps have successfully trapped charged particles in free space by applying an additional field. In the Penning trap, one applies a strong uniform magnetic field, such that the charged particles are confined to a circular orbit via the Lorentz force,
. Using a static electric field with a saddle-point, both Penning and radio-frequency (RF) Paul traps have successfully trapped charged particles in free space by applying an additional field. In the Penning trap, one applies a strong uniform magnetic field, such that the charged particles are confined to a circular orbit via the Lorentz force,  . The RF Paul trap applies a time-varying voltage to its electrodes, which produce a saddle potential that oscillates sinusoidally as a function of time. This rapid change of sign allows for certain ions to be trapped because for particular charge to mass ratios, the effective focusing force is stronger than the defocussing force.
. The RF Paul trap applies a time-varying voltage to its electrodes, which produce a saddle potential that oscillates sinusoidally as a function of time. This rapid change of sign allows for certain ions to be trapped because for particular charge to mass ratios, the effective focusing force is stronger than the defocussing force.
If the ions remain close to the nulls of the potential, then the micromotion of the ions is small, and it is a good approximation to describe the system via a static pseudopotential that approximates the trapping effect of the time-varying potential. We use the numerical modeling software Comsol to simulate this effective pseudopotential that arises from applying a time-varying voltage to the RF ring and additional DC voltages on the other electrodes. The effective total potential energy,  , of an ion in the oblate Paul trap can be approximated by
, of an ion in the oblate Paul trap can be approximated by

where  is the effective pseudopotential due to the RF fields and
is the effective pseudopotential due to the RF fields and  is the additional potential due to the DC voltage applied on the top and bottom electrodes and the RF ring. The resulting pseudopotential at a certain point in space will depend upon the RF frequency,
is the additional potential due to the DC voltage applied on the top and bottom electrodes and the RF ring. The resulting pseudopotential at a certain point in space will depend upon the RF frequency,  , and the RF electric field amplitude,
, and the RF electric field amplitude,  , at that point [45] and is given by
, at that point [45] and is given by

which depends on the charge, q, and the mass, m, of the particular ion being trapped. After simulating the field using Comsol, we find that the electric field amplitude from the RF field near the trap center can be approximated by

where  is the amplitude of the RF voltage. Plugging this into Eq. (3) yields
is the amplitude of the RF voltage. Plugging this into Eq. (3) yields

where  is a fitting parameter, that is determined by grounding the top and bottom electrodes and numerically modeling the square of the RF electric field amplitude, as shown in Figure 2. We calculate the DC electric field as having 3 contributions: one from the voltage applied to the RF ring,
is a fitting parameter, that is determined by grounding the top and bottom electrodes and numerically modeling the square of the RF electric field amplitude, as shown in Figure 2. We calculate the DC electric field as having 3 contributions: one from the voltage applied to the RF ring,  , one from the voltage applied to the top electrodes,
, one from the voltage applied to the top electrodes,  and one from the bottom electrodes,
and one from the bottom electrodes,  . The DC voltage on the RF ring,
. The DC voltage on the RF ring,  , is given by
, is given by

where  is the DC voltage on the ring.
is the DC voltage on the ring.
Numerical results for the pseudopotential produced by applying our anticipated operating parameters of a
500
V RF
amplitude and a RF frequency of
35
MHz, and grounding the top and bottom electrodes. The oblate Paul trap’s edges are shown as solid magenta lines. For our anticipated parameters the pseudopotential well depth is 1.6 eV. This numerical result is used to calculate  . (a) The pseudopotential is shown in the
. (a) The pseudopotential is shown in the  plane. The dashed magenta line identifies the plane of panel (b). (b) The pseudopotential is shown in the
plane. The dashed magenta line identifies the plane of panel (b). (b) The pseudopotential is shown in the  plane and the dashed magenta line shows the plane of panel (a).
plane and the dashed magenta line shows the plane of panel (a).
We numerically model the electrostatic potential due to the DC voltage applied to the either the top or bottom electrodes, as shown in Figure 3. We find that near the trap center, the numerical results for the electrostatic potential produced by a voltage of  the top or bottom electrodes is reasonably modeled by the polynomial
the top or bottom electrodes is reasonably modeled by the polynomial

with fitting parameters  ,
,  ,
,  ,
,  ,
,  . Due to the symmetry of the oblate Paul trap, the parameters satisfy
. Due to the symmetry of the oblate Paul trap, the parameters satisfy  .
.
Grounding the RF ring and applying
1 V to the top electrodes, we plot the numerical electric potential. The oblate Paul trap’s electrodes are shown as the solid magenta lines. (a) In the  plane the electrostatic potential due to the top electrodes has a gradient along the
plane the electrostatic potential due to the top electrodes has a gradient along the  direction. This gradient produces an electrostatic force that confines the ions in the center of the trap. (The dashed magenta line shows the plane of panel (b).) (b) The electrostatic potential is shown in the
direction. This gradient produces an electrostatic force that confines the ions in the center of the trap. (The dashed magenta line shows the plane of panel (b).) (b) The electrostatic potential is shown in the  plane, where the dashed magenta line shows the plane of panel (a). For the actual DC voltage applied to the trap, we multiply the potential by actual voltage difference.
plane, where the dashed magenta line shows the plane of panel (a). For the actual DC voltage applied to the trap, we multiply the potential by actual voltage difference.
We can use the results from Eqs. (5)-(7) in Eq. (2) to yield the final effective potential energy of an ion in this oblate Paul trap

Since the effective potential energy is just a function of  , it is rotationally symmetric around the
, it is rotationally symmetric around the  -axis and we would expect there to be a zero frequency rotational mode in the phonon eigenvectors. That mode can be lifted from zero by breaking the symmetry, which can occur by adding additional fields that do not respect the cylindrical symmetry, and probably occur naturally due to imperfections in the trap, the optical access ports, stray fields, etc.
-axis and we would expect there to be a zero frequency rotational mode in the phonon eigenvectors. That mode can be lifted from zero by breaking the symmetry, which can occur by adding additional fields that do not respect the cylindrical symmetry, and probably occur naturally due to imperfections in the trap, the optical access ports, stray fields, etc.
3 Equilibrium structure and normal modes
Using Eq. (8) (the calculated pseudopotential), we solve for the equilibrium structure of the crystal in the standard way. We first construct an initial trial configuration for the ions and then minimize the total potential energy of the oblate Paul trap (including the trap potential and the Coulomb repulsion between ions), as summarized in Eq. (9); MatLab is used for the nonlinear minimization with a multidimensional Newton’s method. We rewrite the total potential energy of the oblate Paul trap in a conventional form (up to a constant) via

where  . Here
. Here  is the ith component of the nth ion’s location and
is the ith component of the nth ion’s location and  . The frequencies in Eq. (9) are defined via
. The frequencies in Eq. (9) are defined via



We will express all distances in terms of a characteristic length,  , which satisfies
, which satisfies

and we will work with dimensionless coordinates  when calculating the equilibrium positions. Furthermore, we measure all frequencies relative to
when calculating the equilibrium positions. Furthermore, we measure all frequencies relative to  . The normalized frequencies are
. The normalized frequencies are

for  ,
,  ,
,  , and
, and  . The dimensionless total potential energy becomes
. The dimensionless total potential energy becomes

where we have defined  and
and  .
.
To find the equilibrium positions, we use the gradient of the total potential energy and numerically minimize the total potential energy using a multidimensional Newton’s method. The gradient of Eq. (9) is

The force on ion m in the  direction will be
direction will be  . We seek the solution in which all ions lie in a plane parallel to the
. We seek the solution in which all ions lie in a plane parallel to the  plane, such that
plane, such that  for all
for all  . As a result of this condition,
. As a result of this condition,  , and there is no
, and there is no  contribution to the Coulomb potential term. The value of
contribution to the Coulomb potential term. The value of  is determined by setting the
is determined by setting the  term equal to zero in Eq. (16) and is given by the condition
term equal to zero in Eq. (16) and is given by the condition

Using  , the ion equilibrium positions are numerically obtained when all 3N components of the force on each ion are zero, which is given by
, the ion equilibrium positions are numerically obtained when all 3N components of the force on each ion are zero, which is given by  .
.
After the equilibrium positions  are found, we expand the total potential about the equilibrium positions up to quadratic order
are found, we expand the total potential about the equilibrium positions up to quadratic order

The nonzero terms of the expansion are the zeroth order and the quadratic terms; the first order term is zero because the equilibrium position is defined to be where the gradient of the total potential is zero, however the zeroth term is also neglected since it is a constant. We calculate the Lagrangian of the trapped ions using the quadratic term of the Taylor expanded total potential, with  being the dimensionless displacement from the equilibrium position for the nth ion in the ith direction. The expanded Lagrangian becomes
being the dimensionless displacement from the equilibrium position for the nth ion in the ith direction. The expanded Lagrangian becomes

where  represents the elements of the effective spring constant matrices which are given by
represents the elements of the effective spring constant matrices which are given by



where  and
and  is the planar interparticle distance between ions n and m. Note that motion in the 3-direction (axial direction) is decoupled from motion in the
is the planar interparticle distance between ions n and m. Note that motion in the 3-direction (axial direction) is decoupled from motion in the  plane.
plane.
After applying the Euler-Lagrange equation to Eq. (19) and substituting the eigenvector solution  , we are left to solve the standard eigenvalue equation
, we are left to solve the standard eigenvalue equation

There are two sets of normal modes: eigenvectors of the  matrix
matrix  yield the ‘axial’ modes (those corresponding to motion perpendicular to the crystal plane) and eigenvectors of the
yield the ‘axial’ modes (those corresponding to motion perpendicular to the crystal plane) and eigenvectors of the  matrix
matrix  ,
,  , yield the ‘planar’ modes (those corresponding to ion motion in the crystal plane).
, yield the ‘planar’ modes (those corresponding to ion motion in the crystal plane).
4 Results
Now that we have constructed the formal structure to determine the equilibrium positions, phonon eigenvectors, and phonon frequencies, and we have determined the total pseudopotential of the trap, we are ready to solve these systems of equations to determine the expected behavior of the trapped ions. We present several numerical examples to illustrate the equilibrium structure, eigenvalues of the normal modes, and the effective spin-spin interaction  for the axial modes with a detuning of the spin-dependent optical dipole force above the axial center-of-mass phonon frequency,
for the axial modes with a detuning of the spin-dependent optical dipole force above the axial center-of-mass phonon frequency,  . We use an ytterbium ion with mass
. We use an ytterbium ion with mass  , where u is the atomic mass unit, and a positive charge
, where u is the atomic mass unit, and a positive charge  . For the frequency of the RF voltage, we use
. For the frequency of the RF voltage, we use  and the amplitude of the potential applied to the RF ring is
and the amplitude of the potential applied to the RF ring is  . The DC voltage applied to the RF ring and to the top and bottom electrodes will be
. The DC voltage applied to the RF ring and to the top and bottom electrodes will be  . We work in a region where the trapped ion configurations are stable. The ion crystal is stable only when both
. We work in a region where the trapped ion configurations are stable. The ion crystal is stable only when both  and
and  are real and nonzero, as defined in Eq. (14) and this region is shown in Figure 4, which depends on the voltages applied to the RF ring and to the top and bottom electrodes. We work with ion crystals that contain up to 20 ions.
are real and nonzero, as defined in Eq. (14) and this region is shown in Figure 4, which depends on the voltages applied to the RF ring and to the top and bottom electrodes. We work with ion crystals that contain up to 20 ions.
 and
and
 are both real when the ion configuration is stable (shaded grey). We use Eq. (14) to find a region where the ion configuration is stable. The white regions are unstable.
are both real when the ion configuration is stable (shaded grey). We use Eq. (14) to find a region where the ion configuration is stable. The white regions are unstable.
4.1 Equilibrium configurations
A single ion will sit in the center of the trap. As more ions are added, because the ions repel each other, a ‘hard core’ like structure will form, starting with rings of ions until it becomes energetically more stable to have one ion in the center of the ring, and then additional shells surrounding it, and so on. We find that as we increase the number of ions, the single ring is stable for  . Increasing N further creates more complex structures. We show the common equilibrium configurations for
. Increasing N further creates more complex structures. We show the common equilibrium configurations for  with DC voltages of
with DC voltages of  and
and  , in Figure 5. As mentioned above,
, in Figure 5. As mentioned above,  is the last configuration that is comprised of a single ring of ions, as depicted in Figure 5(a). The
is the last configuration that is comprised of a single ring of ions, as depicted in Figure 5(a). The  configuration is ideal to use in order to study when periodic boundary conditions are applied to the linear chain, this is due to the configuration being in a single ring. For configurations with
configuration is ideal to use in order to study when periodic boundary conditions are applied to the linear chain, this is due to the configuration being in a single ring. For configurations with  through 8, the additional ions are added to an outer ring. When
through 8, the additional ions are added to an outer ring. When  the additional ions are added to the center. In Figure 5(b),
the additional ions are added to the center. In Figure 5(b),  is the first configuration that forms a ring in the center, with three ions. The equilibrium configuration of
is the first configuration that forms a ring in the center, with three ions. The equilibrium configuration of  is the maximum number to have two rings, as shown in Figure 5(c). Ion configurations with
is the maximum number to have two rings, as shown in Figure 5(c). Ion configurations with  have a single ion at the center, as an example of this, we show
have a single ion at the center, as an example of this, we show  in Figure 5(d). The common configurations for
in Figure 5(d). The common configurations for  are nearly formed from triangular lattices (up to nearest neighbor) and this could be used to study frustration in the effective spin models (except, of course, that due to the finite number of ions there are many cases where the coordination number of an interior ion is not equal to 6, as seen in Figure 5). The shape of all of these clusters for small N agree with those found in Ref. [39], except for
are nearly formed from triangular lattices (up to nearest neighbor) and this could be used to study frustration in the effective spin models (except, of course, that due to the finite number of ions there are many cases where the coordination number of an interior ion is not equal to 6, as seen in Figure 5). The shape of all of these clusters for small N agree with those found in Ref. [39], except for  , which have small differences due to the different potential that describes the oblate Paul trap from the potential used in [39].
, which have small differences due to the different potential that describes the oblate Paul trap from the potential used in [39].
Equilbrium positions (blue dots) calculated for
 (a),
10
(b),
15
(c),
20
(d) with
(a),
10
(b),
15
(c),
20
(d) with
 and
and
 . (a)
. (a)  is the maximum number of ions for a single ring. (b)
is the maximum number of ions for a single ring. (b)  is the first instance where there is a second ring in the center of the configuration. (c) Similar to panel (a),
is the first instance where there is a second ring in the center of the configuration. (c) Similar to panel (a),  is the maximum number of ions to have two rings. (d)
is the maximum number of ions to have two rings. (d)  is the maximum number ions expected to operate within our trap. As previously noted, the additional ions when added to the
is the maximum number ions expected to operate within our trap. As previously noted, the additional ions when added to the  equilibrium configuration occupy the outer rings instead of the center.
equilibrium configuration occupy the outer rings instead of the center.
We next show the dependence of the equilibrium positions on the DC voltages applied to the RF ring and independently applied to the top and bottom electrodes. We fix  . As each DC voltage is independently varied, the shape of the equilibrium configuration for
. As each DC voltage is independently varied, the shape of the equilibrium configuration for  remains the same and only the distances between ions change, as shown in the four cases in Figure 6. The equilibrium positions are robust to when
remains the same and only the distances between ions change, as shown in the four cases in Figure 6. The equilibrium positions are robust to when  as shown in Figure 6(c), although this voltage setting will not be used due to the effects of micromotion. The enhanced micromotion is due to the plane of the trapped ions are no longer at the center of the trap but at some offset. This offset of the plane will expose the ions to a stronger restoring force.
as shown in Figure 6(c), although this voltage setting will not be used due to the effects of micromotion. The enhanced micromotion is due to the plane of the trapped ions are no longer at the center of the trap but at some offset. This offset of the plane will expose the ions to a stronger restoring force.
4.2 Normal modes
After determining the equilibrium positions, we can find the spring constants and then solve the eigenvalue problem to find the normal modes. Note that due to rotational symmetry, there always is a zero frequency planar mode corresponding to the free rotation of the crystal. In an actual experiment, however, we expect that the rotational symmetry of the trap will be broken by stray fields, the radial optical access tunnels, imperfections in the electrodes, etc., so that mode will be lifted from zero.
We show the eigenvalues of the normal modes for  in Figure 7. In Figure 7 for a given
in Figure 7. In Figure 7 for a given  ,
,  , and
, and  there are 5 axial phonon frequencies, however the axial phonon frequencies has two pairs of degenerate modes. One degenerate pair are the two orthogonal tilt modes and the other pair is the two orthogonal zig-zag modes. Similarly there are 10 planar phonon frequencies, however there are 4 pairs that are degenerate. The axial phonon frequencies decrease as the DC voltage on the RF ring increases and the planar phonon frequencies decrease as the DC voltage on the RF ring decreases. For the majority of the combinations of
there are 5 axial phonon frequencies, however the axial phonon frequencies has two pairs of degenerate modes. One degenerate pair are the two orthogonal tilt modes and the other pair is the two orthogonal zig-zag modes. Similarly there are 10 planar phonon frequencies, however there are 4 pairs that are degenerate. The axial phonon frequencies decrease as the DC voltage on the RF ring increases and the planar phonon frequencies decrease as the DC voltage on the RF ring decreases. For the majority of the combinations of  and
and  the axial phonon frequencies lie in a narrow band that is separated from the planar mode frequencies, which also lie in a narrow band. As
the axial phonon frequencies lie in a narrow band that is separated from the planar mode frequencies, which also lie in a narrow band. As  increases the axial band broadens and eventually overlaps the planar band, which is also broadening. This behavior of the axial phonon frequencies and planar phonon frequencies occurs when
increases the axial band broadens and eventually overlaps the planar band, which is also broadening. This behavior of the axial phonon frequencies and planar phonon frequencies occurs when  as shown in Figure 7(c), although this voltage setting will not be used due to the micromotion which is larger in this case. When the axial band has an eigenvalue that goes soft, the system is no longer stable within one plane (which is the equivalent of the zig-zag transition in the linear Paul trap). When
as shown in Figure 7(c), although this voltage setting will not be used due to the micromotion which is larger in this case. When the axial band has an eigenvalue that goes soft, the system is no longer stable within one plane (which is the equivalent of the zig-zag transition in the linear Paul trap). When  the initial clustering of the axial modes and planar modes is not present, as shown in Figure 7(a).
the initial clustering of the axial modes and planar modes is not present, as shown in Figure 7(a).
Eigenvalues of the normal modes as a function of
 for
for
 . The axial mode frequencies (blue circles) decrease and planar mode frequencies (red triangles) increase as
. The axial mode frequencies (blue circles) decrease and planar mode frequencies (red triangles) increase as  increases, as shown in the four cases illustrated: (a)
increases, as shown in the four cases illustrated: (a)  , (b)
, (b)  , (c)
, (c)  and
and  and (d)
and (d)  . For (b)-(d) the eigenvalues of the normal modes also are closer together at low
. For (b)-(d) the eigenvalues of the normal modes also are closer together at low  and separate as
and separate as  increases. The axial frequencies have two degeneracies and the planar frequencies have four degeneracies as discussed in the main text.
increases. The axial frequencies have two degeneracies and the planar frequencies have four degeneracies as discussed in the main text.
4.3 Ising spin-spin interaction
The ions in our trap have two hyperfine states that are separated by a frequency  . Three laser beams with two beatnotes at frequencies
. Three laser beams with two beatnotes at frequencies  will illuminate the ions, selectively exciting phonon modes as described in [3]. In this case, we choose the laser beams to propagate along the
will illuminate the ions, selectively exciting phonon modes as described in [3]. In this case, we choose the laser beams to propagate along the  direction, as defined in Figure 1(b), such that the laser beams are insensitive to the micromotion which is entirely radial. The phonon modes are excited in a spin-dependent way to generate effective spin-spin interactions which can be described by the Ising spin coupling matrix,
direction, as defined in Figure 1(b), such that the laser beams are insensitive to the micromotion which is entirely radial. The phonon modes are excited in a spin-dependent way to generate effective spin-spin interactions which can be described by the Ising spin coupling matrix, 

where  is the Pauli spin matrix of ion i in the
is the Pauli spin matrix of ion i in the  -direction and we have neglected the time-dependent terms of the spin couplings
-direction and we have neglected the time-dependent terms of the spin couplings  . The explicit formula for
. The explicit formula for  is [46]
is [46]

where the coefficient  , depends on the carrier transition Rabi frequency (Ω), the difference in wavevector between the laser beams (δk), the ion mass (m), and the frequency of the center-of-mass mode, (
, depends on the carrier transition Rabi frequency (Ω), the difference in wavevector between the laser beams (δk), the ion mass (m), and the frequency of the center-of-mass mode, ( ), and is given by
), and is given by

We calculate the spin-spin coupling, using Eq. (25), for a small number of ions in order to neglect the micromotion and assume the ions are at their average position. The micromotion will be approximately equal to the displacement of the ion from the RF null times the Mathieu q-parameter [47]. The ions with the largest micromotion will occur in the outermost ‘ring’ of the crystal. For N ions and an average inter-ion spacing s, the ions in the outermost ring are a distance  from the center, which means that the amplitude of the micromotion is approximately
from the center, which means that the amplitude of the micromotion is approximately  , and the ratio of this micromotion amplitude to the inter-ion spacing is therefore
, and the ratio of this micromotion amplitude to the inter-ion spacing is therefore  .
.
It is expected that if one detunes, μ, to be larger than the center-of-mass mode frequency, then one can generate long-range spin-spin couplings that vary as a power law from 0 to 3, as they decay with distance [14, 15, 48]. Hence, we fit the spin-spin couplings to a power law in distance as a function of detuning in Figure 8 for  . Note that our system is still rather small, so there are likely to be finite size effects that modify the simple power law behavior.
. Note that our system is still rather small, so there are likely to be finite size effects that modify the simple power law behavior.
The trap could also be use the recent work on a controlled phase flip (CPF) quantum gate that includes the corrections due to the micromotion and is optimized to attain high fidelity [16]. The high fidelity is obtained by dividing the time of the gate into m equal segments, during each segment of equal time a particular Rabi frequency is applied,  (
( ), that has been optimized for the βth segment. The optimized
), that has been optimized for the βth segment. The optimized  are determined by solving the motional dynamics, that explicitly take into account all the micromotion contributions. The motion of the ions are described by a set of coupled time-dependent Mathieu equations.
are determined by solving the motional dynamics, that explicitly take into account all the micromotion contributions. The motion of the ions are described by a set of coupled time-dependent Mathieu equations.
4.4 Quantum motional effects
The trap could also be used to examine different types of quantum motional effects of ions, similar to the recent work on the Aharonov-Bohm effect [26]. In order to examine such effects, one would need to cool the system to nearly the ground state. This can be accomplished by including Raman side-band cooling after Doppler cooling the system for all modes except the soft rotational mode, at least when the potential is large enough that the mode frequencies are sizeable. To cool the rotational mode, one would need to add a perturbation to the system that lifts the phonon mode frequency, side-band cool it, and then adiabatically reduce the frequency by removing the perturbation. This procedure will cool off that phonon mode, which can yield quite small quanta in it [26]. Once the system has been prepared in this state, then quantum tunneling effects, or coherent motional effects could be studied in the trap for a range of different ion configurations. It might also be interesting to extend these types of studies to cases where the ions no longer lie completely in one plane, but have deformed into a full three-dimensional structure (as long as the larger micromotion does not cause problems). Finally, many of these ideas would need to be used if one tried to examine time crystals, especially the cooling of the rotational mode to be able to see quantum effects [27, 28].
5 Conclusion
In this work, we have studied 2D ion crystals in an oblate Paul trap for use in quantum simulations. With this system, one can trap a modest number of ions in 2D planar structures that are likely to be highly frustrated without needing a Penning trap, providing a controlled way to study the onset of frustration effects in quantum simulations. We calculated the equilibrium positions and the phonon frequencies for the proposed oblate Paul trap over its stable region. The equilibrium positions with  form a single ring configuration and could potentially be used to study periodic boundary conditions and the Aharonov-Bohm effect when
form a single ring configuration and could potentially be used to study periodic boundary conditions and the Aharonov-Bohm effect when  (and possibly time crystals). Once
(and possibly time crystals). Once  , the equilibrium configurations have multiple rings that are nearly formed from triangular lattices. One can generate an effective Ising Hamiltonian by driving axial modes with a spin-dependent optical dipole force. When detuning is to the blue of the axial center-of-mass mode, the spin-spin coupling,
, the equilibrium configurations have multiple rings that are nearly formed from triangular lattices. One can generate an effective Ising Hamiltonian by driving axial modes with a spin-dependent optical dipole force. When detuning is to the blue of the axial center-of-mass mode, the spin-spin coupling,  , has an approximate power law that is within the expected range of 0 to 3. In the future, as this trap is tested and performs simulations of spin models with ions, the work presented here will be critical to determining the parameters of the Hamiltonian and for selecting the appropriate configurations to use in the different simulations.
, has an approximate power law that is within the expected range of 0 to 3. In the future, as this trap is tested and performs simulations of spin models with ions, the work presented here will be critical to determining the parameters of the Hamiltonian and for selecting the appropriate configurations to use in the different simulations.
References
Feynman R: Simulating physics with computers. Int. J. Theor. Phys. 1982,21(6/7):467–488.
Friedenauer A, Schmitz H, Glueckert J, Porras D, Schaetz T: Simulating a quantum magnet with trapped ions. Nat. Phys. 2008,4(10):757–761. 10.1038/nphys1032
Kim K, Chang M-S, Korenblit S, Islam R, Edwards E, Freericks J, Lin G-D, Duan L-M, Monroe C: Quantum simulation of frustrated Ising spins with trapped ions. Nature 2010,465(7268):590–593.
Islam R, Edwards E, Kim K, Korenblit S, Noh C, Carmichael H, Lin G-D, Duan L-M, Wang C-C, Freericks J, Monroe C: Onset of a quantum phase transition with a trapped ion quantum simulator. Nat. Commun. 2011, 2:377.
Islam R, Senko C, Campbell W, Korenblit S, Smith J, Lee A, Edwards E, Wang C-C, Freericks J, Monroe C: Emergence and frustration of magnetism with variable-range interactions in a quantum simulator. Science 2013,340(6132):583–587. 10.1126/science.1232296
Lanyon B, Hempel C, Nigg D, Müller M, Gerritsma R, Zähringer F, Schindler P, Barreiero J, Rambach M, Kirchmair G, Hennrich M, Zoller P, Blatt R, Roos C: Universal digital quantum simulation with trapped ions. Science 2011,334(6052):57–61. 10.1126/science.1208001
Senko C, Smith J, Richerme P, Lee A, Campbell W, Monroe C: Coherent imaging spectroscopy of a quantum many-body spin system. Science 2014, 345:430. 10.1126/science.1251422
Richerme P, Gong Z-X, Lee A, Senko C, Smith J, Foss-Feig M, Michalakis S, Gorshkov A, Monroe C: Non-local propagation of correlations in long-range interacting quantum systems. Nature 2014, 511:198. 10.1038/nature13450
Jurcevic P, Lanyon B, Hauke P, Hempel C, Zoller P, Blatt R, Roos C: Observation of entanglement propagation in a quantum many-body system. Nature 2014, 511:202. 10.1038/nature13461
Wuerker RF, Shelton H, Langmuir RV: Electrodynamic containment of charged particles. J. Appl. Phys. 1959,30(3):342. 10.1063/1.1735165
Casdroff R, Blatt R: Ordered structures and statistical properties of ion clouds stored in a Paul trap. Appl. Phys. B 1988, 45:175–182. 10.1007/BF00695288
Walther H: From a single ion to a mesoscopic system - crystallization of ions in Paul traps. Phys. Scr. 1995, 59:360–368.
Landa H, Drewsen M, Reznik B, Retzker A: Classical and quantum modes of coupled Mathieu equations. J. Phys. A, Math. Theor. 2012., 45: Article ID 455305
Porras D, Cirac J: Effective quantum spin systems with trapped ions. Phys. Rev. Lett. 2004.,92(20): Article ID 207901
Britton J, Sawyer B, Keith A, Wang C-C, Freericks J, Uys H, Biercuk M, Bollinger J: Engineered two dimensional Ising interactions in a trapped-ion quantum simulator with hundreds of spins. Nature 2012,484(7395):489–492. 10.1038/nature10981
Shen C, Duan L-M: High fidelity quantum gates for trapped ions under micromotion. Phys. Rev. A 2014., 90: Article ID 022332
Clark R, Lin T, Brown K, Chuang I: A two-dimensional lattice ion trap for quantum simulation. J. Appl. Phys. 2009.,105(1): Article ID 013114
Sterling R, Rattanasonti H, Weidt S, Lake K, Srinivasan P, Webster S, Kraft M, Hensinger W: Fabrication and operation of a two-dimensional ion-trap lattice on a high-voltage microchip. Nat. Commun. 2014, 5:3637.
Chiaverini J, Lybarger W: Laserless trapped-ion quantum simulations without spontaneous scattering using microtrap arrays. Phys. Rev. A 2008.,77(2): Article ID 022324
Kumph M, Brownnutt M, Blatt R: Two-dimensional arrays of radio-frequency ion traps with addressable interactions. New J. Phys. 2011., 13: Article ID 073043
Siverns J, Weidt S, Lake K, Lekitsch B, Hughes M, Hensinger W: Optimization of two-dimensional ion trap arrays for quantum simulation. New J. Phys. 2012., 14: Article ID 085009
Schmied R, Wesenberg J, Leibfried D: Optimal surface-electrode trap lattices for quantum simulation with trapped ions. Phys. Rev. Lett. 2009.,102(23): Article ID 233002
Korenblit S, Kafri D, Campbell W, Islam R, Edwards E, Gong Z-X, Lin G-D, Duan L-M, Kim J, Kim K, Monroe C: Quantum simulation of spin models on an arbitrary lattice with trapped ions. New J. Phys. 2012., 14: Article ID 095024
Yoshimura B, Campbell W, Freericks J: Diabatic ramping spectroscopy of many-body excited states for trapped-ion quantum simulators. Phys. Rev. A 2014 (to appear).
del Campo A, Rams M, Zurek W: Assisted finite-rate adiabatic passage across a quantum critical point: exact solution for the quantum Ising model. Phys. Rev. Lett. 2012.,109(11): Article ID 115703
Noguchi A, Shikano Y, Toyoda K, Urabe S: Aharonov-Bohm effect in the tunnelling of a quantum rotor in a linear Paul trap. Nat. Commun. 2014, 5:3868.
Wilcek F: Quantum time crystals. Phys. Rev. Lett. 2012.,109(16): Article ID 160401
Li T, Gong Z-X, Yin Z-Q, Quan H, Yin X, Zhang P, Duan L-M, Zhang X: Space-time crystals of trapped ions. Phys. Rev. Lett. 2012.,109(16): Article ID 163001
Itano W, Bergquist J, Wineland D: Coulomb clusters of ions in a Paul trap. In Proceedings of the Workshop on Crystalline Ion Beams: 4–7 October 1988; Wertheim, Germany Edited by: Hasse R, Hofmann I, Liese D. 1989, 241.
Bergquist J, Wineland D, Itano W, Hemmati H, Daniel H, Leuchs G:Energy and radiative lifetime of the

 state in Hg II by Doppler-free two-photon laser spectroscopy.
Phys. Rev. Lett. 1985,55(15):1567–1570. 10.1103/PhysRevLett.55.1567
state in Hg II by Doppler-free two-photon laser spectroscopy.
Phys. Rev. Lett. 1985,55(15):1567–1570. 10.1103/PhysRevLett.55.1567Wineland D, Itano W, Bergquist J, Hulet R: Laser-cooling limits and single-ion spectroscopy. Phys. Rev. A 1987,36(5):2220–2231. 10.1103/PhysRevA.36.2220
Bergquist J, Hulet R, Itano WM, Wineland D: Observation of quantum jumps in a single atom. Phys. Rev. Lett. 1986,57(14):1699–1702. 10.1103/PhysRevLett.57.1699
Wineland D, Itano W, Bergquist J: Absorption spectroscopy at the limit: detection of a single atom. Opt. Lett. 1987,12(6):389–391. 10.1364/OL.12.000389
Bergquist J, Itano W, Wineland D: Recoilless optical absorption and Doppler sidebands of a single trapped ion. Phys. Rev. A 1987,36(1):428–431. 10.1103/PhysRevA.36.428
Heinzen D, Wineland D: Quantum-limited cooling and detection of radio-frequency oscillations by laser-cooled ions. Phys. Rev. A 1990,42(5):2977–3004. 10.1103/PhysRevA.42.2977
Block M, Drakoudis A, Leuthner H, Seibert P, Werth G: Crystalline ion structures in a Paul trap. J. Phys. B 2000,33(11):375–382. 10.1088/0953-4075/33/11/101
Kaufmann H, Ulm S, Jacob G, Poschinger U, Landa H, Retzker A, Plenio MB, Schmidt-Kaler F: Precise experimental investigation of eigenmodes in a planar ion crystal. Phys. Rev. Lett. 2012., 109: Article ID 263003
Schiffer J: Phase transitions in anisotropically confined ionic crystals. Phys. Rev. Lett. 1993,70(6):818. 10.1103/PhysRevLett.70.818
Bedanov V, Peeters F: Ordering and phase transitions of charged particles in a classical finite two-dimensional system. Phys. Rev. B 1994,49(4):2667–2676.
Buluta I, Kitaoka M, Georgescu S, Hasegawa S: Investigation of planar coulomb crystals for quantum simulation and computation. Phys. Rev. A 2008.,77(6): Article ID 062320
Buluta I, Hasegawa S: The structure of planar coulomb crystals in rf traps. J. Phys. B, At. Mol. Opt. Phys. 2009.,42(15): Article ID 154004
Clossen T, Roussel M: The flattening phase transition in systems of trapped ions. Can. J. Chem. 2009,87(10):1425–1435. 10.1139/V09-116
Landa H, Drewsen M, Reznik B, Retzker A: Modes of oscillation in radiofrequency Paul traps. New J. Phys. 2012., 14: Article ID 093023
Landa H, Retzker A, Schaetz T, Reznik B: Entanglement generation using discrete solitons inWigner crystals. e-print 2014. arXiv: 1308.2943
Dehmelt H: Radiofrequency spectroscopy of stored ions I: storage. 3. In Advances in Atomic and Molecular Physics. Edited by: Bates D, Estermann I. Academic Press, New York; 1967:53–72.
Zhu S-L, Monroe C, Duan L-M: Trapped ion quantum computation with transverse phonon modes. Phys. Rev. Lett. 2006.,97(5): Article ID 050505
Berkeland DJ, Miller JD, Bergquist JC, Itano WM, Wineland DJ: Minimization of ion micromotion in a Paul trap. J. Appl. Phys. 1998, 83:5025. 10.1063/1.367318
Senko C, Smith J, Richerme P, Lee A, Campbell WC, Monroe C: Coherent imaging spectroscopy of a quantum many-body spin system. Science 2014, 345:430. 10.1126/science.1251422
Acknowledgements
We thank Dr. Philippe Bado, Dr. Mark Dugan and Dr. Christopher Schenck of Translume (Ann Arbor, MI) for valuable discussions. B.Y. acknowledges the Achievement Rewards for College Scientists Foundation for supporting this work. M.S. acknowledges the National Science Foundation under grant number DMR-1004268 for support. J.K.F. and B.Y. acknowledge the National Science Foundation under grant number PHY-1314295 for support. D.D. and W.C.C. acknowledge support from the U.S. Air Force Office of Scientific Research Young Investigator Program under grant number FA9550-13-1-0167 and support from the AFOSR STTR Program. J.K.F. also acknowledges support from the McDevitt bequest at Georgetown University.
Author information
Authors and Affiliations
Corresponding author
Additional information
Competing interests
The authors declare that they have no competing interests.
Authors’ contributions
The idea from this work came from Wes Campbell and Jim Freericks. Danilo Dadic and Wes Campbell developed the electric field potentials for the pseudopotential description of the trap as well as designing the trap parameters. Bryce Yoshimura, Marybeth Stork and Jim Freericks performed all of the theoretical calculations. The paper manuscript was first drafted by Bryce Yoshimura and then all authors contributed to revisions.
Rights and permissions
Open Access This article is distributed under the terms of the Creative Commons Attribution 4.0 International License (https://creativecommons.org/licenses/by/4.0), which permits use, duplication, adaptation, distribution, and reproduction in any medium or format, as long as you give appropriate credit to the original author(s) and the source, provide a link to the Creative Commons license, and indicate if changes were made.
About this article
Cite this article
Yoshimura, B., Stork, M., Dadic, D. et al. Creation of two-dimensional Coulomb crystals of ions in oblate Paul traps for quantum simulations. EPJ Quantum Technol. 2, 2 (2015). https://doi.org/10.1140/epjqt14
Received:
Accepted:
Published:
DOI: https://doi.org/10.1140/epjqt14






 and
and  and
and  , (c)
, (c)  ,
,  and
and 

 and
and
 and different number of ions (different panels; (a) is
and different number of ions (different panels; (a) is
 and (b) is
and (b) is
 ) on a log-log plot. The colored lines are the fit to a power-law behavior
) on a log-log plot. The colored lines are the fit to a power-law behavior  . The detunings are
. The detunings are  to the blue of
to the blue of 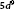

 state in Hg II by Doppler-free two-photon laser spectroscopy.
Phys. Rev. Lett. 1985,55(15):1567–1570. 10.1103/PhysRevLett.55.1567
state in Hg II by Doppler-free two-photon laser spectroscopy.
Phys. Rev. Lett. 1985,55(15):1567–1570. 10.1103/PhysRevLett.55.1567